Hi Scott!
Thank you very much on your clear explanation and a nice example 
Now I understand the difference between two opcodes. I was using eqfil as a “standard” bandpass filter but actually butterbp is what I needed.
If anyone else lands here with a similar problem here is a simple equaliser example with a GUI (made in Cabbage but can be easily transferred to anywhere else) that can be used as a starting point:
<Cabbage>
form caption("5-band Equaliser") size(400, 420), guiMode("queue"), pluginId("def1")
keyboard bounds(10, 302, 382, 95) channel("keyboard2")
rslider bounds(0, 198, 82, 80) channel("gain_0") range(-60, 10, 0, 1, 0.01) valueTextBox(1) fontColour(0, 0, 0, 255)
rslider bounds(80, 200, 82, 80) channel("gain_1") range(-60, 10, 0, 1, 0.01) valueTextBox(1) fontColour(0, 0, 0, 255)
rslider bounds(160, 200, 82, 80) channel("gain_2") range(-60, 10, 0, 1, 0.01) valueTextBox(1) fontColour(0, 0, 0, 255)
rslider bounds(240, 200, 82, 80) channel("gain_3") range(-60, 10, 0, 1, 0.01) valueTextBox(1) fontColour(0, 0, 0, 255)
rslider bounds(320, 200, 82, 80) channel("gain_4") range(-60, 10, 0, 1, 0.01) valueTextBox(1) fontColour(0, 0, 0, 255)
vslider bounds(-30, 54, 150, 150) channel("level_0") range(0, 80, 20, 1, 0.1) active(0) colour(0, 0, 0, 0)
vslider bounds(50, 54, 150, 150) channel("level_1") range(0, 80, 20, 1, 0.1) active(0) colour(0, 0, 0, 0)
vslider bounds(130, 54, 150, 150) channel("level_2") range(0, 80, 20, 1, 0.1) active(0) colour(0, 0, 0, 0)
vslider bounds(210, 54, 150, 150) channel("level_3") range(0, 80, 20, 1, 0.1) active(0) colour(0, 0, 0, 0)
vslider bounds(290, 54, 150, 150) channel("level_4") range(0, 80, 20, 1, 0.1) active(0) colour(0, 0, 0, 0)
label bounds(30, 280, 24, 16) channel("label_0") text("dB")
label bounds(110, 280, 24, 16) channel("label_1") text("dB")
label bounds(190, 280, 24, 16) channel("label_2") text("dB")
label bounds(270, 280, 24, 16) channel("label_3") text("dB")
label bounds(350, 280, 24, 16) channel("label_4") text("dB")
label bounds(32, 0, 338, 46) channel("title_label") text("EQ+Monitor")
</Cabbage>
<CsoundSynthesizer>
<CsOptions>
-n -d -+rtmidi=NULL -M0 -m0d --midi-key-cps=4 --midi-velocity-amp=5
</CsOptions>
<CsInstruments>
; Initialize the global variables.
ksmps = 32
nchnls = 2
0dbfs = 1
;instrument will be triggered by keyboard widget
instr 1
kgains[] init 5
kgains[0] = cabbageGetValue:k("gain_0")
kgains[1] = cabbageGetValue:k("gain_1")
kgains[2] = cabbageGetValue:k("gain_2")
kgains[3] = cabbageGetValue:k("gain_3")
kgains[4] = cabbageGetValue:k("gain_4")
// Define cutoff frequency of a lowpass filter
klc = 100 // in Hz
// Define the central frequencies and bandwidths for pass band filters
kcf[] fillarray 300, 1200, 3500 // in Hz
kbw[] fillarray 300, 1000, 2500 // in Hz
// Define cutoff frequency of a highpass filter
khc = 8000 // in Hz
// Arrays initialization
aEqOuts[] init 5
aBandOuts[] init 5
kBandLvls[] init 5
// sound synthesis
aOut poscil p5, p4
// EQ filtering
//aEqOuts[0] butterbp aOut, kcf[0], kbw[0]
aEqOuts[0] butterlp aOut, klc
aEqOuts[1] butterbp aOut, kcf[0], kbw[0]
aEqOuts[2] butterbp aOut, kcf[1], kbw[1]
aEqOuts[3] butterbp aOut, kcf[2], kbw[2]
aEqOuts[4] butterhp aOut, khc
// Apply band gains
aRes = 0 // resulting audio vector
kIndx = 0
while (kIndx < lenarray(aEqOuts)) do
aBandOuts[kIndx] = aEqOuts[kIndx] * ampdb(kgains[kIndx])
aRes += aBandOuts[kIndx]
kIndx += 1
od
// Calculate RMS for monitor
kBandLvls[0] rms aBandOuts[0]
kBandLvls[1] rms aBandOuts[1]
kBandLvls[2] rms aBandOuts[2]
kBandLvls[3] rms aBandOuts[3]
kBandLvls[4] rms aBandOuts[4]
// Monitor (GUI) update
kIndx = 0
while (kIndx < lenarray(aEqOuts)) do
Schann sprintfk "level_%d", kIndx
kMonitorVal = dbamp(kBandLvls[kIndx]) + 70
cabbageSetValue Schann, kMonitorVal
kIndx += 1
od
// envelope generation
kEnv madsr .1, .2, .6, .4
// write output to output buffer
outs aRes*kEnv, aRes*kEnv
endin
</CsInstruments>
<CsScore>
f0 z
</CsScore>
</CsoundSynthesizer>
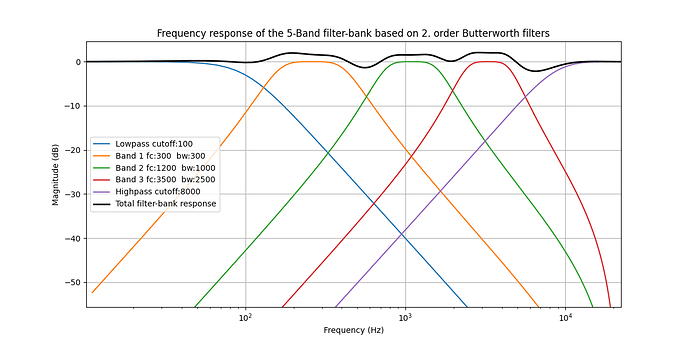
I’m pretty sure that this filterbank is not the best one so if anyone wants to experiment a bit with different ones e.g. with different central frequencies and bandwidths or different number bands, here is a python script that will plot its frequency response:
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import butter, freqz
# Define cutoff frequency of a lowpass filter
lowcutoff = 100 # in Hz
# Define the central frequencies and bandwidths for pass band filters
central_frequencies = [300, 1200, 3500] # in Hz
bandwidths = [300, 1000, 2500] # in Hz
# Define cutoff frequency of a highpass filter
highcutoff = 8000 # in Hz
# Sampling frequency and order of the Butterworth filters
fs = 44100 # Sample rate in Hz
order = 2 # Order of the Butterworth filters
nyquist = 0.5 * fs
# Construct the filter bank
filter_bank = []
# construct lowpass filter
b, a = butter(order, lowcutoff/nyquist, btype='low')
filter_bank.append((b, a))
# construct bandpass filters
for center, bandwidth in zip(central_frequencies, bandwidths):
lowcut = center - bandwidth / 2
highcut = center + bandwidth / 2
low = lowcut / nyquist
high = highcut / nyquist
b, a = butter(order, [low, high], btype='band')
filter_bank.append((b, a))
# construct highpass filter
b, a = butter(order, highcutoff/nyquist, btype='high')
filter_bank.append((b, a))
# Plot the frequency response of each filter
plt.figure(figsize=(12, 6))
for b, a in filter_bank:
w, h = freqz(b, a, fs=fs)
plt.plot(w, 20 * np.log10(np.abs(h)))
# Calculate and plot the sum of all responses
total_response = np.zeros_like(w)
for b, a in filter_bank:
w, h = freqz(b, a, fs=fs)
total_response += np.abs(h)
plt.plot(w, 20 * np.log10(total_response), 'k', linewidth=2)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude (dB)')
plt.title(f'Frequency response of the 5-Band filter-bank based on {order}. order Butterworth filters')
plt.xscale('log')
plt.legend([f'Lowpass cutoff:{lowcutoff}',
f'Band 1 fc:{central_frequencies[0]} bw:{bandwidths[0]}',
f'Band 2 fc:{central_frequencies[1]} bw:{bandwidths[1]}',
f'Band 3 fc:{central_frequencies[2]} bw:{bandwidths[2]}',
f'Highpass cutoff:{highcutoff}',
'Total filter-bank response'])
plt.grid(True)
plt.show()
Please correct me if I’m wrong here, basically the flatter the frequency response the better but, that being said, more important is that you know what you have; in this case that would be